Theory Seminar
Arnold Filtser: Clan Embeddings into Trees, and Low Treewidth Graphs
Arnold FiltserBar-Ilan University
WHEN:
Wednesday, November 17, 2021 @ 12:30 pm - 1:30 pm
This event is free and open to the publicAdd to Google Calendar
This event is free and open to the publicAdd to Google Calendar
WEB: Event Website
SHARE:
In low distortion metric embeddings, the goal is to embed a host “hard” metric space into a “simpler” target space while approximately preserving pairwise distances. A highly desirable target space is that of a tree metric. Unfortunately, such embedding will result in a huge distortion.
A celebrated bypass to this problem is stochastic embedding with logarithmic expected distortion. Another bypass is Ramsey-type embedding, where the distortion guarantee applies only to a subset of the points. However, both these solutions fail to provide an embedding into a single tree with a worst-case distortion guarantee on all pairs.
A celebrated bypass to this problem is stochastic embedding with logarithmic expected distortion. Another bypass is Ramsey-type embedding, where the distortion guarantee applies only to a subset of the points. However, both these solutions fail to provide an embedding into a single tree with a worst-case distortion guarantee on all pairs.
In this paper, we propose a novel third bypass called clan embedding. Here each point 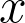 is mapped to a subset of points
is mapped to a subset of points ) , called a clan, with a special chief point
, called a clan, with a special chief point %5Cin%09f(x)) . The clan embedding has multiplicative distortion
. The clan embedding has multiplicative distortion 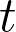 if for every pair
if for every pair ) some copy
some copy ) in the clan of
in the clan of 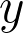 is close to the chief of
is close to the chief of 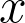 :
: %7Dd(y',%5Cchi(x))%5Cle%09t%5Ccdot%09d(x,y)) . Our first result is a clan embedding into a tree with multiplicative distortion
. Our first result is a clan embedding into a tree with multiplicative distortion ) such that each point has
such that each point has  copies (in expectation). In addition, we provide a “spanning” version of this theorem for graphs and use it to devise the first compact routing scheme with constant size routing tables.We then focus on minor-free graphs of diameter parameterized by
copies (in expectation). In addition, we provide a “spanning” version of this theorem for graphs and use it to devise the first compact routing scheme with constant size routing tables.We then focus on minor-free graphs of diameter parameterized by  , which were known to be stochastically embeddable into bounded treewidth graphs with expected additive distortion
, which were known to be stochastically embeddable into bounded treewidth graphs with expected additive distortion 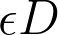 . We devise Ramsey-type embedding and clan embedding analogs of the stochastic embedding. We use these embeddings to construct the first (bicriteria quasi-polynomial time) approximation scheme for the metric
. We devise Ramsey-type embedding and clan embedding analogs of the stochastic embedding. We use these embeddings to construct the first (bicriteria quasi-polynomial time) approximation scheme for the metric 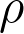 -dominating set and metric
-dominating set and metric 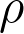 -independent set problems in minor-free graphs.
-independent set problems in minor-free graphs.
Joint work with Hung Le
 MENU
MENU 
