Theory Seminar
New Approximation Bounds for Small-Set Vertex Expansion
Suprovat GhoshalNorthwestern / TTIC
WHERE:
3725 Beyster BuildingMap
WHEN:
Friday, January 12, 2024 @ 2:00 pm - 3:00 pm
This event is free and open to the publicAdd to Google Calendar
This event is free and open to the publicAdd to Google Calendar
WEB: Event Website
SHARE:
(Passcode: 430018)
The vertex expansion of the graph is a fundamental graph parameter. Given a graph ) and a parameter
and a parameter ![\delta \in (0,1/2] \delta \in (0,1/2]](https://s0.wp.com/latex.php?zoom=3&bg=ffffff&fg=000000&s=0&latex=%5Cdelta%09%5Cin%09(0,1/2]) , its
, its 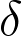 -Small-Set Vertex Expansion (SSVE) is defined as
-Small-Set Vertex Expansion (SSVE) is defined as
where is the vertex boundary of a set
. The SSVE problem, in addition to being of independent interest as a natural graph partitioning problem, is also of interest due to its connections to the StrongUniqueGames Problem (Ghoshal-Louis’21). We give a randomized algorithm running in time
, which outputs a set
of size
, having vertex expansion at most
where is the largest vertex degree of the graph, and
is the optimal
-SSVE. The previous best-known guarantees for this were the bi-criteria bounds of
and
due to Louis-Makarychev [TOC’16].
Our algorithm uses the basic SDP relaxation of the problem augmented with ) rounds of the Lasserre/SoS hierarchy. Our rounding algorithm is a combination of the rounding algorithms of Raghavendra-Tan’12 and Austrin-Benabbas-Georgiou’13. A key component of our analysis is novel Gaussian rounding lemma for hyperedges, which might be of independent interest.
rounds of the Lasserre/SoS hierarchy. Our rounding algorithm is a combination of the rounding algorithms of Raghavendra-Tan’12 and Austrin-Benabbas-Georgiou’13. A key component of our analysis is novel Gaussian rounding lemma for hyperedges, which might be of independent interest.
This is joint work with Anand Louis.
 MENU
MENU 
